Achsensymmetrie zur y-Achse
Die Achsensymmetrie zur y-Achse ist eine wichtige Eigenschaft von Funktionen. In diesem Artikel werden wir uns ausführlich mit diesen Inhalten auseinandersetzen und dir alles Wissenswerte dazu vermitteln. Wir werden erklären, was die Achsensymmetrie zur y-Achse bedeutet, wie du diese Eigenschaft bestimmen kannst und welche Bedeutung sie für die Graphen von ganzrationalen Funktionen hat.
Was ist die Achsensymmetrie zur y-Achse
Eine Funktion f(x) ist zur y-Achse achsensymmetrisch, wenn sie für alle x-Werte denselben Funktionswert wie für -x liefert. Dies bedeutet, dass das Ergebis gleich sein muss, wenn du zum Beispiel 3 und die -3 einsetzt \(f(3)=f(-3)\), genauso wie \(f(4)=f(-4)\), \(f(5)=f(-5)\) usw. Mit anderen Worten, die Funktion ist spiegelsymmetrisch zur y-Achse. Graphisch bedeutet das, dass die y-Achse eine Spiegelachse ist.
Achsensymmetrie zur y-Achse bei ganzrationalen Funktionen direkt erkennen
Um zu bestimmen, ob eine ganzrationale Funktion achsensymmetrisch zur y-Achse ist, müssen wir die Gleichung der Funktion betrachten. Wenn alle Exponenten der Variablen in der Gleichung gerade sind, dann ist die Funktion zur y-Achse achsensymmetrisch. Wenn mindestens ein Exponent ungerade ist, ist die Funktion nicht achsensymmetrisch zur y-Achse. Ein Absolutglied, also eine reine Zahl ohne x am Ende, darf vorkommen!
Beispiel:
\(f(x) = x^4 – 3x^2 + 2\quad \rightarrow\) Alle Exponenten in dieser Funktion sind gerade, daher ist die Funktion zur y-Achse achsensymmetrisch.
\(f(x) = x^4 – 3x^2 +4x+ 2\quad \rightarrow\) Alle Exponenten in dieser Funktion sind nicht gerade ( da \(x=x^1\) und die 1 ist eine ungerade Zahl), daher ist die Funktion nicht achsensymmetrisch zur y-Achse.

Graphische Bedeutung der Achsensymmetrie zur y-Achse
Die Achsensymmetrie zur y-Achse bedeutet, dass eine Funktion oder ein Graph spiegelbildlich zur y-Achse verläuft. Das heißt, wenn man eine senkrechte Linie durch den Graphen zieht, welche auf der y-Achse liegt, dann sind die Punkte auf der einen Seite dieser Linie spiegelbildlich zu den Punkten auf der anderen Seite. Die senkrechte y-Achse dient also als eine Art “Spiegel”.
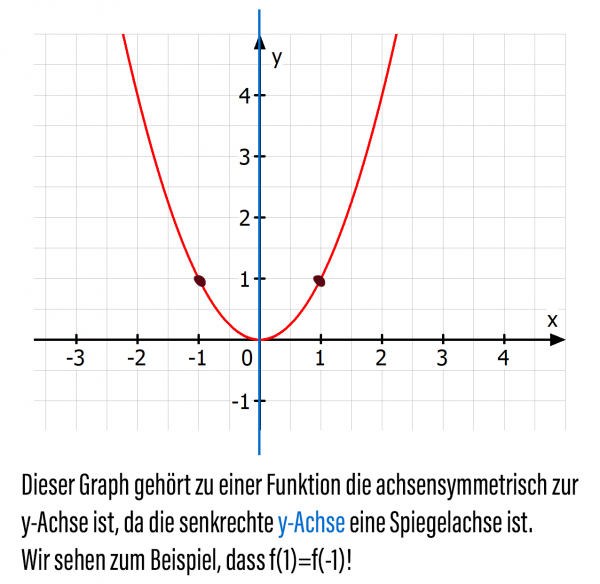
Beispiele (rechnerischer Nachweis) Achsensymmetrie zur y-Achse:
Natürlich gibt es auch einen rechnerischen Nachweis für achsensymmetrische Funktionen. Hierzu bildet man \(f(-x)\) und vergleicht dieses Ergebnis mit der Ausgangsfunktion. Stimmen die gebildete Funktion und die Ausgangsfunktion überein, dann ist die vorliegende Funktion symmetrisch zur y-Achse, andernfalls nicht.
Doch wie wird f(-x) gebildet?
Hierzu ersetzt man jedes vorkommdende x in der Ausgangsfunktion durch \((-x)\). Dieser Ausdruck wird dann vereinfacht. Beachte bitte, dass beim Vereinfachen die Potenzen Vorrang haben. Wenn man also \(2(-x)^4\) vereinfachen soll, dann liegt das erste Augenmerk auf \((-x)^4\). Die Potenz geht schließlich vor! \((-x)^4\) steht für \((-x)\cdot (-x)\cdot (-x)\cdot (-x)\) und dies ergibt \(x^4\). Das Ganze mit Zwei multipliziert ist \(2x^4\).
Beispiel 1:
Um zu untersuchen, ob die Funktion \(f(x) = x^4 – 3x^3 + 1\) achsensymmetrisch zur y-Achse ist, müssen wir zeigen, dass \(f(x) = f(-x)\) gilt. Das bedeutet, dass der Funktionswert für \(x\) gleich dem Funktionswert für \(-x\) sein muss. Also setzen wir \(-x\) für \(x\) in die Funktion \(f(x)\) ein und vergleichen die Gleichung mit der ursprünglichen Funktion:
\begin{align*} f(x) &= x^4 – 3x^3 + 1\\
f(-x) &= (-x)^4 – 3(-x)^3 + 1\\
&= x^4 – 3(-x)^3 + 1\\
&= x^4 + 3x^3 + 1 \end{align*}
Wenn die Funktion achsensymmetrisch zur y-Achse ist, dann müsste gelten: \(f(x) = f(-x)\). Aber wie wir sehen können, ist \(f(x) \neq f(-x)\), da die Gleichung \(x^4 – 3x^3 + 1 \neq x^4 + 3x^3 + 1\) für einige Werte von \(x\) erfüllt ist.
Daher ist die Funktion \(f(x) = x^4 – 3x^3 + 1\) nicht achsensymmetrisch zur y-Achse.
Beispiel 2:
Um zu überprüfen, ob die Funktion \(f(x) = x^6 – 2x^2 + 5\) achsensymmetrisch zur y-Achse ist, müssen wir schauen, ob \(f(x) = f(-x)\) ist. Wir ersetzen \(x\) durch \(-x\) in der Ausgangsnktion \(f(x)\), vereinfachen anschließend und vergleichen die Gleichung mit der ursprünglichen Funktion:
\begin{align*} f(x) &= x^6 – 2x^2 + 5\\
f(-x) &= (-x)^6 – 2(-x)^2 + 5\\
&= x^6 – 2x^2 + 5 \end{align*}
Da \(f(x) = f(-x)\) gilt, ist die Funktion \(f(x) = x^6 – 2x^2 + 5\) achsensymmetrisch zur y-Achse.
Fehlerquellen bei der Bestimmung der Achsensymmetrie zur y-Achse
Eine mögliche Fehlerquelle bei der Untersuchung auf Achsensymmetrie zur y-Achse ist das ungenaue Prüfen von \(f(x)=f(-x)\). Es kann vorkommen, dass durch Rechenfehler oder ungenaue Schreibweise von Funktionen die Gleichheit nicht korrekt nachgewiesen wird. Insbesondere bei komplexen Funktionen können schnell Fehler gemacht werden, die das Ergebnis verfälschen.
Zudem können auch Funktionen mit ungeraden Exponenten aufgrund ihrer Eigenschaften nicht achsensymmetrisch zur y-Achse sein, obwohl \(f(x)=f(-x)\) gilt. Deshalb ist es wichtig, die Funktionsart zu kennen und nicht nur die Gleichung zu überprüfen. Die Regelung mit den geraden Exponenten gilt nämlich ausschließlich für ganzrationale Funktionen.
FAQ - Achsensymmetrie zur y-Achse
Eine Funktion ist achsensymmetrisch zur y-Achse, wenn ihr Graph nach Spiegelung an der y-Achse ihr Aussehen nicht verändert.
Die Achsensymmetrie zur y-Achse hat einen graphischen Hintergrund, der auf der Symmetrie der Koordinatenachse beruht. Da die y-Achse die Symmetrieachse der Funktion darstellt, müssen die Punkte auf der einen Seite der y-Achse eine Spiegelung auf der anderen Seite der Achse aufweisen.
Um zu zeigen, dass eine Funktion achsensymmetrisch zur y-Achse ist, muss man zeigen, dass sie die Gleichung \(f(x) = f(-x)\) erfüllt. Dies bedeutet, dass der Funktionswert für \(x\) gleich dem Funktionswert für \(-x\) sein muss. Man kann diese Gleichung überprüfen, indem man \(-x\) für \(x\) in die Funktion einsetzt und prüft, ob die Gleichung gilt.
Beispiel: Betrachte die Funktion \(f(x) = x^4 – 3x^3 + 1\). Um zu zeigen, dass diese Funktion nicht achsensymmetrisch zur y-Achse ist, setzen wir \(-x\) für \(x\) in die Funktion ein:
\(f(-x) = (-x)^4 – 3(-x)^3 + 1 = x^4 + 3x^3 + 1\)
Wenn die Funktion achsensymmetrisch zur y-Achse wäre, müsste gelten \(f(x) = f(-x)\). Da dies jedoch nicht der Fall ist, ist die Funktion nicht achsensymmetrisch zur y-Achse.
Eine mögliche Fehlerquelle bei der Untersuchung auf Achsensymmetrie zur y-Achse besteht darin, dass man vergisst, die Gleichung f(x) = f(-x) zu überprüfen. Ein weiterer Fehler kann darin bestehen, dass man die Gleichung falsch umformt oder die Ergebnisse nicht sorgfältig überprüft.
Fazit - Achsensymmetrie zur y-Achse:
Zusammenfassend lässt sich sagen, dass die Achsensymmetrie zur y-Achse ein wichtiges Konzept in der Mathematik ist, das bei der Untersuchung von Funktionen eine große Rolle spielt. Es ist wichtig, die graphische Bedeutung der Symmetrie zu verstehen und den rechnerischen Nachweis mit \(f(x) = f(-x)\) sorgfältig durchzuführen, um mögliche Fehlerquellen zu vermeiden.
Machst du dieses Jahr dein Abitur und suchst nach einer Unterstützung?
Dann schau dir unseren Abikurs an!
Unsere Skripte könnten dich auch interessieren...








