Die PQ-Formel: Wie du quadratische Gleichungen einfach lösen kannst
Wenn du dich schon einmal mit quadratischen Gleichungen beschäftigt hast, hast du sicherlich von der pq-Formel gehört. Aber was genau ist die pq-Formel und wie wird sie angewendet? In diesem Beitrag erfährst du alles, was du über die pq-Formel wissen musst und wie du sie zur Lösung von quadratischen Gleichungen anwendest.
Die pq-Formel:
Die pq-Formel lautet wie folgt:
$$x_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right) ^2-q}$$
Wenn du eine Gleichung in der Form x²+px+q=0 hast, kannst du die pq-Formel anwenden, um die Lösungen zu finden. Dabei steht p für den Koeffizienten, also für die Zahl vor dem x und q für den konstanten Term am Ende (die reine Zahl).
Wir betrachten als Eingangsbeispiel die Gleichung \(x²+2x-3=0\). In diesem Fall ist also p=2 und q=-3. Wir können die pq-Formel wie folgt anwenden:
\begin{align}x_{1,2}&=-\frac{2}{2} \pm \sqrt{\left(\frac{2}{2}\right) ^2-(-3)}\\
x_{1,2} &=-1\pm\sqrt{1+3}\\
x_{1,2} &=-1\pm\sqrt{4}\\
x_{1,2} &=-1\pm 2\\\end{align}
somit ist \(x_1 = 1 \text{ und } x_2 = -3 \)
Die Lösungsmenge lautet \(\mathbb{L} = {\{-3,1\}}.\)
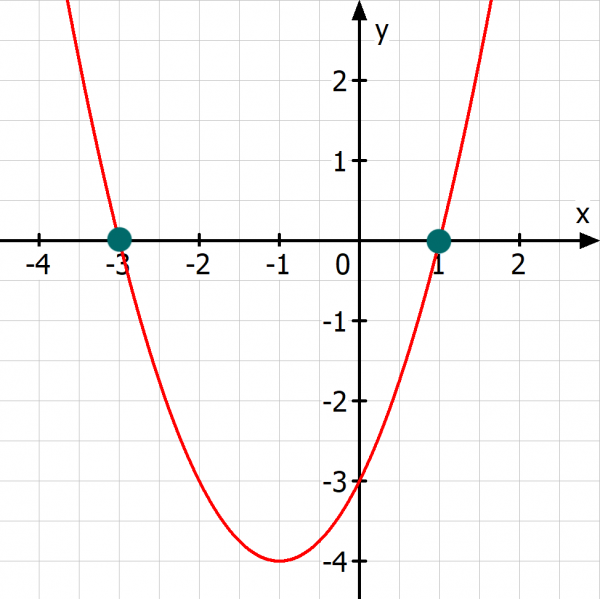
Wenn du eine Gleichung löst bei der das Ergebnis Null ist, dann sind die Lösungen graphisch betrachtet die Schnittstellen des zugehörigen Funktionsgraphen mit der waagerechten x-Achse!
Die Schritte der pq-Formel:
- 1. Schritt: Forme die Gleichung in Normalform \(x^2+px+q=0\) um
- 2. Schritt: Lese nun p und q ab.
- 3. Schritt: Setze die Zahlen für p und q in die Formel ein.
- 4. Schritt: Berechne jetzt die Lösungen.
- 5. Schritt: Schreibe die Lösungsmenge auf.
Gegeben sei die quadratische Gleichung: \( 2x^2 – 4x = 6 \)
1. Schritt: Um die Gleichung in die Normalform \(x^2 + px + q = 0\) zu bringen, ziehen wir auf beiden Seiten \(6\) ab:
\begin{align} 2x^2 – 4x &= 6 \quad \vert\, -6 \\
2x^2 – 4x – 6 &= 0\end{align}
Jetzt müssen wir die Gleichung normieren, indem wir sie durch 2 teilen, denn vor dem \(x^2\) darf keine Zahl stehen:
\begin{align} 2x^2 – 4x – 6 &= 0\quad \vert :2 \\
x^2 – 2x -3 &= 0 \end{align}
2. Schritt: Jetzt können wir p (Zahl vor x) und q (Zahl am Ende) bestimmen:
\begin{equation} p = -2, \qquad q =-3 \end{equation}
3. Schritt: Wir setzen nun in die p-q-Formel ein:
\begin{equation} x_{1,2} = -\frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2}\right)^2 – (-3)} \end{equation}
4. Schritt: Jetzt können wir den Ausdruck vereinfachen und die Lösungen berechnen:
\begin{align} x_{1,2} &= -\frac{-2}{2} \pm \sqrt{\left(\frac{-2}{2}\right)^2 – (-3)} \\
x_{1,2} &= 1 \pm \sqrt{1 + 3} \end{align}
\begin{equation} x_1 = 1 + \sqrt{4} = 3, \qquad x_2 = 1 – \sqrt{4} = -1 \end{equation}
5. Schritt: Daher sind die Lösungen der quadratischen Gleichung \(2x^2 – 4x = 6\) \(x_1 = 3\) und \(x_2 = -1\).
Die Lösungsmenge lautet \(\mathbb{L} = {\{-1,3\}}.\)

Anzahl an Lösungen:
Die Diskriminante spielt eine entscheidende Rolle, um die Anzahl der Lösungen der Gleichung zu bestimmen. Sie ist ein mathematischer Ausdruck, der aus der pq-Formel abgeleitet wird und wird durch den Term \(\left(\frac{p}{2}\right) ^2-q\) (also der Ausruck unter der Wurzel) dargestellt. Die Diskriminante gibt Auskunft darüber, wie viele Lösungen eine quadratische Gleichung hat. Dabei spielt das Vorzeichen der Diskriminante eine wichtige Rolle.
Um die Anzahl der Lösungen einer quadratischen Gleichung mit der pq-Formel zu bestimmen, muss man zuerst die Diskriminante berechnen. Ist die Diskriminante größer als Null, so hat die Gleichung zwei Lösungen. Bei einer Diskriminante von genau Null hat die Gleichung eine doppelte Lösung. Wenn die Diskriminante kleiner als Null ist, hat die Gleichung keine Lösung in den reellen Zahlen.
Anhand dieser Bedingungen kann man also schnell erkennen, wie viele Lösungen eine quadratische Gleichung hat, indem man einfach die Diskriminante berechnet und ihr Vorzeichen überprüft.
Es gilt: \(D=\left(\frac{p}{2}\right)^2-q:\)
- D>0: Es gibt zwei Lösungen
- D=0: Es gibt eine Lösung
- D<0: Die Gleichung hat keine Lösung
Wann ist die pq-Formel sinnvoll/welche Alternativen gibt es
Die pq-Formel ist eine quadratische Lösungsformel. Rein theoretisch kannst sie für alle quadratischen Gleichungen,die in der Normalform gegeben sind verwenden. Manchmal ist sie sinnvoll, manchmal aber auch nicht!
Hier siehst du eine Übersicht über die verschiedenen Arten quadratischer Gleichungen:
1. Reinquadratisch ohne Absolutglied, also ohne reine Zahl am Ende (q = 0, p = 0):
\(x^2 = 0\) oder auch \(3x^2=0\) Hier formst du nach \(x^2\) um und ziehst dann einfach die Wurzel!
2. Reinquadratisch mit Absolutglied (p = 0) \(x^2 + q = 0\):
Wie zum Beispiel \(x^2-16=0\). Hier kannst du nach \(x^2\) umformen und wenn möglich die Wurzel ziehen.
3. Gemischtquadratisch ohne Absolutglied (keine reine Zahl) (q = 0) \(x^2 + px = 0 \):
Wie zum Beispiel \(x^2+4x=0\) Hier eignet sich eher die Ausklammernmethode!
4. Gemischtquadratisch mit Absolutglied \(x^2 + px + q = 0\):
Wie zum Beispiel \( x^2-12x-11=0\) Hier ist die pq-Formel sinnvoll!
Fazit: Die pq-Formel ist besonders sinnvoll bei gemischtquadratische Gleichungen mit Absolutglied zu benutzen. Für die anderen Formen kannst du sie zwar auch verwenden, aber gibt es leichtere Lösungsverfahren, wie zum Beispiel das Umformen nach x oder aber die Ausklammernmethode.
Beispiele zur pq-Formel:
Beispiel 1: Zwei Lösungen
Gegeben sei die Gleichung: \( x^2 – 12x – 13 = 0 \)
Da der Koeffizient von \(x^2\) gleich 1 ist müssen wir nicht normieren und p ist gleich dem Koeffizienten von x, also p=-12.
Außerdem ist q gleich dem Konstantenterm, also q=13.
Wir setzen nun diese Werte in die p-q-Formel ein:
\begin{align}x_{1,2} &= -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 – q}\\
x_{1,2} &= -\frac{-12}{2} \pm \sqrt{\left(\frac{-12}{2}\right)^2 – (-13)} \\
x_{1,2} &= 6 \pm \sqrt{36+13} \\
x_1 &= 6 + \sqrt{49} = 6+7 = 13 \\
x_2 &= 6 – \sqrt{49} = 6-7 = -1 \end{align}
Daher sind die Lösungen der quadratischen Gleichung \(x^2-12x-13=0\) \(x_1 = 13\) und \(x_2 = -1\).
Die Lösungsmenge lautet \(\mathbb{L} = {\{13,-1\}}.\)
Beispiel 2: Eine Lösung
Gegeben sei die quadratische Gleichung: \( x^2 – 10x + 25 = 0 \)
Wir lesen ab: p=-10 und q=25. Und setzen nun in die Formel ein:
\begin{align} x_{1,2} &= -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 – q} \\
x_{1,2} &= -\frac{-10}{2} \pm \sqrt{\left(\frac{-10}{2}\right)^2 – 25} \\
x_{1,2} &= 5 \pm \sqrt{25 – 25}\\
x_{1,2} &= 5 \pm \sqrt{0}\\
x_{1,2} &= 5 \pm 0 \end{align}
Da der Term unter der Wurzel Null ergibt, fällt er weg:
\begin{equation} x_1 = 5, \qquad x_2 = 5 \end{equation}
Daher ist die Lösung der quadratischen Gleichung \(x^2 – 10x + 25 = 0\) \(x_1 = 5\) und \(x_2 = 5\). Beachte, dass in diesem Fall die beiden Lösungen identisch sind, da der quadratische Term vollständig faktorisiert werden kann zu \((x-5)^2\). Die Gleichung hat somit eine doppelte Lösung!
Die Lösungsmenge lautet \(\mathbb{L} = {\{5\}}.\)
Beispiel 3: Keine Lösung
Gegeben sei die quadratische Gleichung: \( x^2 – 4x + 10 = 0 \)
Wir lesen ab: p=-4 und q=10 und setzen nun in die p-q-Formel ein:
\begin{align} x_{1,2} &= -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 – q}\\
x_{1,2} &= -\frac{-4}{2} \pm \sqrt{\left(\frac{-4}{2}\right)^2 – 10} \\
x_{1,2} &= 2 \pm \sqrt{4 – 10}\\
x_{1,2} &= 2 \pm \sqrt{-6} \end{align}
Da die Wurzel negativ ist, gibt es keine Lösung in den reellen Zahlen, sondern nur komplexe Lösungen.
Die Lösungsmenge lautet \(\mathbb{L} = {\{\ \ \ \}}.\)
Herleitung der pq-Formel:
Um die pq-Formel herzuleiten, können wir eine quadratische Gleichung in Normalform \(x^2 + px + q = 0\) durch quadratische Ergänzung nach \(x\) auflösen. Dazu subtrahieren wir \(q\) von beiden Seiten, um die Gleichung in die Form \(x^2 + px = -q\) zu bringen. Anschließend ergänzen wir den Ausdruck \(px\), indem wir auf beiden Seiten \((\frac{p}{2})^2\) hinzufügen. Dadurch erhalten wir \(x^2 + px + (\frac{p}{2})^2 = (\frac{p}{2})^2 – q\). Mit Hilfe der ersten binomischen Formel vereinfachen wir die linke Seite zu \((x + \frac{p}{2})^2 = (\frac{p}{2})^2 – q\). Indem wir die Wurzel auf beiden Seiten ziehen, können wir die Formel weiter umformen, und erhalten \(x + \frac{p}{2} = \pm \sqrt{(\frac{p}{2})^2 – q}\). Nun formen wir weiter nach x um, indem wir \(+\frac{p}{2}\) durch Gegenrechnung auf die andere Seite des Gleichheitszeichens bringen und erhalten somit \(x_{1,2} = -\frac{p}{2} \pm \sqrt{(\frac{p}{2})^2 – q}\). Dadurch erhalten wir die beiden möglichen Lösungen für die quadratische Gleichung.
Fehlerquellen der pq-Formel:
Bei der Anwendung der pq-Formel können verschiedene Fehlerquellen auftreten. Einige häufige Fehlerquellen sind:
- Vorzeichenfehler: Wenn Vorzeichen bei der Ersetzung von p und q in die pq-Formel falsch übernommen werden, kann dies zu falschen Ergebnissen führen.
- Rechenfehler: Da die pq-Formel eine mehrstufige Berechnung erfordert, kann es zu Rechenfehlern kommen. Zum Beispiel kann bei der Berechnung des Ausdrucks unter der Wurzel ein Vorzeichenfehler oder eine falsche Zahl eingesetzt werden.
- Verwechslung von p und q: Es kann vorkommen, dass die Variablen p und q in der pq-Formel versehentlich vertauscht werden. Dadurch wird das Ergebnis verfälscht.
- Negative Diskriminante: Wenn der Ausdruck unter der Wurzel negativ ist, hat die quadratische Gleichung keine reellen Lösungen. Es ist wichtig, dies zu erkennen und nicht versuchen, aus einer negative Zahl eine der Wurzel zu ziehen.
Es ist wichtig, bei der Anwendung der pq-Formel sorgfältig zu arbeiten und Rechen- und Vorzeichenfehler zu vermeiden, um korrekte Ergebnisse zu erhalten.
FAQ
Die pq-Formel ist eine Formel zur Lösung quadratischer Gleichungen der Form \(x^2+px+q=0\). Sie lautet: \(x_{1,2} = -\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2 – q}\), wobei p die Zahl vor x ist und q die reine Zahl am Ende.
In der pq-Formel bezeichnet \(p\) den Koeffizienten vor x und \(q\) den Konstanten Term, also die reine Zahl, in der quadratischen Gleichung \(x^2 + px + q = 0\).
Du solltest die pq-Formel anwenden, wenn du eine quadratische Gleichung in der normierten Form \(x^2 + px + q = 0\) lösen möchtest. Wenn du eine Gleichung in anderer Form hast, musst du sie zuerst in diese Form bringen, bevor du die pq-Formel anwenden kannst.
Bevor du die pq-Formel anwenden kannst, musst du sicherstellen, dass die Gleichung in der normierten Form \(x^2 + px + q = 0\) vorliegt. Wenn die Gleichung nicht bereits in dieser Form ist, musst du sie zuerst umformen. Zum Beispiel musst du die Gleichung nach Null auflösen und danach, wenn vorhanden, die komplette Gleichung durch die Zahl, die vor \(x^2\) steht teilen
Um die pq-Formel anzuwenden, setzt du einfach die Werte für p und q in die Formel ein und berechnest die beiden möglichen Lösungen \(x_1\) und \(x_2\).
Es gibt einige häufige Fehlerquellen bei der Anwendung der pq-Formel, wie zum Beispiel das Vergessen des Vorzeichens von p in der Formel oder das Nicht-Überprüfen, ob der Wurzelterm eine reelle Zahl ergibt. Es ist auch wichtig, sicherzustellen, dass die Gleichung in der normierten Form vorliegt.Hierzu musst du vor dem Herauslesen von p und q die Gleichung durch die Zahl teilen, die vor dem \(x^2\) steht.
Häufige Fehlerquellen bei der pq-Formel sind das Vergessen des Vorzeichens von p in der Formel, das Nicht-Überprüfen, ob der Wurzelterm eine reelle Zahl ergibt, und das Nicht-Überprüfen, ob die beiden Lösungen tatsächlich Lösungen der ursprünglichen Gleichung sind.
Du kannst überprüfen, ob die pq-Formel korrekt angewendet wurde, indem du die beiden möglichen Lösungen \(x_1\) und \(x_2\) in die ursprüngliche Gleichung einsetzt und überprüfst, ob sie die Gleichung erfüllen. Nach dem einsetzen in die Gleichung musst du also nach Vereinfachung \(0=0\) erhalten.
Die pq-Formel gibt uns die Lösungen einer quadratischen Gleichung in der Form \(x^2+px+q=0\). Geometrisch gesehen sind die Lösungen die x-Koordinaten der Schnittpunkte der zugehörigen Parabel mit der x-Achse.
Die Diskriminante (der Ausdruck unter der Wurzel) in der pq-Formel entscheidet dabei über die Anzahl der Schnittpunkte. Ist die Diskriminante größer als 0, so hat die Parabel zwei Schnittpunkte mit der x-Achse, was bedeutet, dass es zwei Lösungen für die Gleichung gibt. Ist die Diskriminante gleich 0, so hat die Parabel nur einen Schnittpunkt mit der x-Achse, was bedeutet, dass es eine doppelte Lösung für die Gleichung gibt. Ist die Diskriminante kleiner als 0, so hat die Parabel keine Schnittpunkte mit der x-Achse, was bedeutet, dass es keine reellen Lösungen für die Gleichung gibt.
Fazit
Die pq-Formel ist eine nützliche Methode zur Lösung von quadratischen Gleichungen. Mit Hilfe der pq-Formel kannst du schnell und einfach die Lösungen einer quadratischen Gleichung bestimmen. Beachte jedoch, dass die pq-Formel nur bei quadratischen Gleichungen angewendet werden kann und sie besonders bei Gleichungen der Form \(x^2+px+q=0\) sinnvoll ist. Möchtest du sie dennoch auf andere quadratische Gleichungen anwenden? Kein Problem. Hier erfährst du wie das funktioniert:
- pq-Formel: ohne Zahl am Ende (ohne q)
- pq-Formel: ohne Zahl vor x
- pq-Formel ohne x
Eine Alternative zur pq-Formel ist die Mitternachtsformel (oder auch abc-Formel). Hier kannst du alles zur Mitternachtsformel nachlesen!




