In diesem Beitrag geht es um den sogenannten Hypothesentest.
Inhalt des Beitrags:
(1.) Wofür ist der Hypothesentest (2.) Der Ablauf des Hypothesentestes (3.) Beispiel: Beidseitiger Test (4.) Beispiel: Linksseitiger Test (5.) Beispiel: Rechtsseitiger Test
(1.) Wofür ist der Hypothesentest?
Bei einem Hypothesentest stehen zunächst zwei sich einander widersprechende Behauptungen, \(H_0\) und \(H_1\) gegenüber. Der Hypothesentest dient dazu, anhand des Ergebnisses einer Stichprobe zu entscheiden, welche dieser Behauptungen richtig und welche falsch, also abzulehnen, ist.
(2.) Der Ablauf des Hypothesentest
Jeder Hypothesentest erfolgt nach einem festen Schema:
Schritt 1: Die Hypothesen \(H_0\) und \(H_1\) aufstellen
Schritt 2: Entscheiden welche Art von einem Hypothesentest vorliegt.
Schritt 3: Erwartungswert und Standardabweichung berechnen
Schritt 4: Irrtumswahrscheinlichkeit
Schritt 5: Entscheidungsregel aufstellen
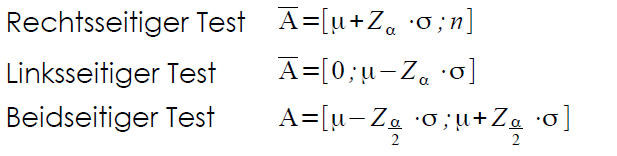
(3.) Beispiel: Der beidseitige Hypothesentest
Situationsbeschreibung:
Ich behaupte: In NRW lieben genau 60% der Menschen Currywurst-Pommes. Es werden 1000 Menschen bei einem Signifikanzniveau von 10% befragt. In dieser Stichprobe sind es 520 Menschen. Habe ich recht?
Schritt 1: Die Hypothesen \(H_0\) und \(H_1\) aufstellen
\(H_0: p=0,6\) und \(H_1: p \neq 0,6\)
Da ich behaupte, dass es genau 60% sind, ist \(p=0,6\).
Die Gegenbehauptung ist somit:
Es sind nicht 60% \( \rightarrow p \neq 0,6 \)
Schritt 2: Entscheiden welcher Test vorliegt
Da \(H_1\) über die Art des Testes entscheidet, liegt hier ein beidseitiger Hypothesentest vor.
Schritt 3: Erwartungswert und Standardabweichung berechnen
\( \begin{array}[h]{ll}
\mu &= n \cdot p = 1000 \cdot 0,6 = 600 \\
\sigma &=\sqrt{ n \cdot p \cdot (1-p)}=\sqrt{ 1000 \cdot 0,6 \cdot (1-0,6)} \\
& = \sqrt{240} \approx 15,5 \end{array}\)
Schritt 4: Irrtumswahrscheinlichkeit
\( \alpha = 10 \%\)
Im beidseitigem Test gilt:
\( Z_{\frac{\alpha}{2}}=Z_{\frac{10\%}{2}}= Z_{5 \%}=1,64 \)
Schritt 5: Entscheidungsregel aufstellen
Berechnung der unteren Grenze:
\( \mu – Z_{\frac {\alpha}{2}} \cdot \sigma= 600 – 1,64 \cdot 15,5 \approx 574,85\)
\( \rightarrow \) Die untere Grenze wird immer aufgerundet: \(575\)
Berechnung der oberen Grenze:
\( \mu + Z_{\frac {\alpha}{2}} \cdot \sigma= 600 + 1,64 \cdot 15,5 \approx 625,42\)
\( \rightarrow \) Die obere Grenze wird immer abgerundet: \(625\)
Annahmebereich: \( A=[575;625]\)
Ablehnungsbereich: \( \bar{A}= [0;574] \cup [626;1000]\)
Da \( 520\) Teil des Ablehnungsbereiches ist, wird meine Behauptung abgelehnt. Ich habe also unrecht.
(4.) Beispiel: Der linksseitige Hypothesentest
Situationsbeschreibung:
Dr. Schmitt behauptet, dass mindestens \( 25\% \) der Raucher an Lungenkrebs erkranken. Hierzu werden 100 Raucher untersucht. Es stellt sich heraus, dass insgesamt 21 Raucher erkrankt sind. Hat Dr. Schmitt bei einer Irrtumswahrscheinlichkeit von \( 10\% \) recht?
Schritt 1: Die Hypothesen \(H_0\) und \(H_1\) aufstellen
\(H_0: p \geq 0,25\) und \(H_1: p < 0,25\)
Da Dr. Schmitt behauptet, dass es mindestens 25% sind, ist \(p \geq 0,25\).
Die Gegenaussage ist somit:
Es sind weniger als 25% \( \rightarrow p < 0,25 \)
Schritt 2: Entscheiden welcher Test vorliegt
Da \(H_1\) über die Richtung des Testes entscheidet, handelt es sich hierbei um einen linksseitigen Hypothesentest.
Schritt 3: Erwartungswert und Standardabweichung berechnen
\( \begin{array}[h]{ll}
\mu &= n \cdot p = 100 \cdot 0,25 = 25 \\
\sigma &=\sqrt{ n \cdot p \cdot (1-p)}=\sqrt{ 100 \cdot 0,25 \cdot (1-0,25)} \\
& = \sqrt{18,75} \approx 4,33 \end{array}\)
Schritt 4: Irrtumswahrscheinlichkeit
\( \alpha = 10 \%\)
Es gilt:
\( Z_\alpha=Z_{10\%}= 1,28 \)
Schritt 5: Entscheidungsregel aufstellen
Die untere Grenze des Ablehnungsbereiches ist bei einem linksseitigen Test immer 0!
Berechnung der oberen Grenze des Ablehnungsbereiches:
\( \mu – Z_{\alpha} \cdot \sigma= 25 – 1,28 \cdot 4,33 \approx 19,46\)
\( \rightarrow \) Die obere Grenze wird immer abgerundet: \(19\)
Ablehnungsbereich: \( \bar{A}= [0;19] \)
Annahmebereich: \( A=[20;100]\)
Da \( 21\) Teil des Annahmebereiches ist, hat Dr. Schmitt recht!
(5.) Beispiel: Der rechtsseitige Hypothesentest
Situationsbeschreibung:
Sonja behauptet, dass höchstens \( 20 \%\) der Schülerinnen und Schüler ihrer Schule Mathe mögen. Ich sage es sind mehr! Hierzu befragen wir unter einem Signifikanzniveau von \( 5 \%\) 100 Schülerinnen und Schüler ihrer Schule. Es geben 27 Schülerinnen und Schüler an, dass sie Mathe mögen. Hat Sonja recht?
Schritt 1: Die Hypothesen \(H_0\) und \(H_1\) aufstellen
\(H_0: p \leq 0,2\) und \(H_1: p > 0,2\)
Höchstens 20% bedeutet: \(p \leq 0,2\)
Die Gegenaussage ist somit:
Es sind mehr als 20% \( \rightarrow p > 0,2 \)
Schritt 2: Entscheiden welcher Test vorliegt
Hierbei handelt es sich um einen rechtsseitigen Hypothesentest, da die \(H_1\)-Hypothese darüber entscheidet und sie rechts von der \(H_0\)-Hypothese und dem Erwartungswert liegt.
Schritt 3: Erwartungswert und Standardabweichung berechnen
\( \begin{array}[h]{ll}
\mu &= n \cdot p = 100 \cdot 0,2 = 20 \\
\sigma &=\sqrt{ n \cdot p \cdot (1-p)}=\sqrt{ 100 \cdot 0,2 \cdot (1-0,2)} \\
& = \sqrt{16} = 4 \end{array}\)
Schritt 4: Irrtumswahrscheinlichkeit
\( \alpha = 5 \%\)
Es gilt:
\( Z_\alpha=Z_{5\%}= 1,64 \)
Schritt 5: Entscheidungsregel aufstellen
Die obere Grenze des Ablehnungsbereiches ist bei einem rechtsseitigen Test immer n, hier also 100!
Berechnung der unteren Grenze des Ablehnungsbereiches:
\( \mu + Z_{\alpha} \cdot \sigma= 20 + 1,64 \cdot 4 = 26,56\)
\( \rightarrow \) Die untere Grenze wird immer aufgerundet: \(27\)
Ablehnungsbereich: \( \bar{A}= [27;100] \)
Annahmebereich: \( A=[0;26]\)
Da \( 27\) Teil des Ablehnungsbereiches ist, wird Sonjas \(H_0\)-Hypothese verworfen. Sie hat also nicht recht!
