In diesem Beitrag lernst du einerseits was Extrema sind und andererseits, wie man diese mithilfe der ersten und zweiten Ableitung berechnet. Am Ende dieses Beitrages findest du außerdem eine kleine Zusammenfassung und eine Übung.
[one_third]Benötigtes Vorwissen:[/one_third][two_third_last]Funktionen ableiten
Lösungsstrategien: pq-Formel, Ausklammern-Methode, Substitution, …[/two_third_last]
[one_third]Übersicht:[/one_third][two_third_last]Graphische Bedeutung der Extrema
In 4 Schritten zu den Koordinaten der Exrema
Beispiele
Übungsaufgaben
Zusammenfassung
weitere Hilfestellung (folgt*)[/two_third_last]
Graphische Bedeutung der Extrema:
[one_half]
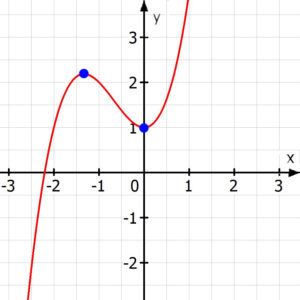
[/one_half][one_half_last]Extrema sind die Hoch- und Tiefpunkte (bzw. Maxima und Minima) einer Funktion.
In diesen Punkten ändert sich die Steigung von steigend nach fallend (oder anders herum).
Ihre Berechnung ist Teil der Kurvendiskussion und kann mithilfe der ersten und zweiten Ableitung erfolgen.[/one_half_last]
In 4 Schritten zu den Koordinaten der Extrema
- $f'(x)$ und $f^{\prime\prime}(x)$ bilden
- notwendige Bedingung: $f'(x)=0$ → Nullstellen der ersten Ableitung berechnen
- hinreichende Bedingung: $f^{\prime\prime}(x)\neq 0$ → Zuvor berechnete Nullstellen in die zweite Ableitung einsetzen und ausrechnen. Ergebnis deuten: $f^{\prime\prime}(x_0)>0$ → Tiefpunkt und $f^{\prime\prime}(x_0)<0$ → Hochpunkt
- y-Koordinate(n) berechnen → Nullstellen (aus Schritt 2) in die Ausgangsfunktion einsetzen und ausrechnen (Ergebnisse sind die zugehörigen y-Koordinaten)
Beispiel 1:
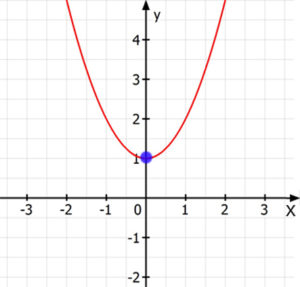
Berechne die Extremwerte der Funktion $f(x)=x^2+1$
1.) $f'(x)$ und $f^{\prime\prime}(x)$ bilden
$f(x)=x^2+1$
$f'(x)=2x$
$f^{\prime\prime}(x)=2$
2.) notwendige Bedingung $f'(x)=0$
\begin{align*}
2x&=0&&\color{red}|\color{red}:\color{red}2\\
x&=0
\end{align*}
3.) hinreichende Bedingung $f^{\prime\prime}(x) \neq 0$
\begin{align*}
&&f^{\prime\prime}(x)&=2\\
&&f^{\prime\prime}(0)&=2&&\color{red}>\color{red}0\color{red}\rightarrow \color{red}T\color{red}P
\end{align*}
4.) y-Koordinate berechnen
$f(0)=0^2+1=1\rightarrow TP(0/1)$
Beispiel 2:
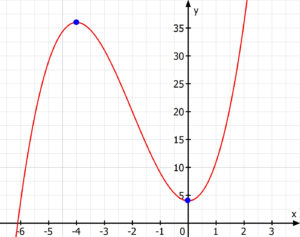
Berechne die Extremwerte der Funktion $f(x)=x^3+6x^2+4$
1.) $f'(x)$ und $f^{\prime\prime}(x)$ bilden
$f(x)=x^3+6x^2+4$
$f'(x)=3x^2+12x$
$f^{\prime\prime}(x)=6x+12$
2.) notwendige Bedingung $f'(x)=0$
\begin{align*}3x^2+12x&=0&&\color{red}|\color{red}(\color{red})\\
x\cdot(3x+12)&=0&&\color{red}|\color{red}S\color{red}v\color{red}N\color{red}P\\\\
\rightarrow x=0 &&3x+12&=0&&\color{red}|\color{red}-\color{red}1\color{red}2\\
&&3x&=-12&&\color{red}|\color{red}:\color{red}3\\&&x&=-4\end{align*}
3.) hinreichende Bedingung $f^{\prime\prime}(x) \neq 0$
$f^{\prime\prime}(x)=6x+12\\$
$f^{\prime\prime}(0)=6\cdot0+12=12\color{red}>\color{red}0\color{red}\rightarrow \color{red}T\color{red}P\\$
$f^{\prime\prime}(-4)=6\cdot(-4)+12=-12\color{red}<\color{red}0 \color{red}\rightarrow \color{red}H\color{red}P$
4.) y-Koordinate berechnen
$f(0)=0^3+6\cdot0^2+4=4 \hspace{1cm}\rightarrow TP(0/4)\\$
$f(-4)=(-4)^3+6\cdot(-4)^2+4=36 \hspace{1cm}\rightarrow HP(-4/36)$
Übungsaufgaben:
[spoiler title=’ 1. Berechne die Extrema von $f(x)=3x^2+6$ (Lösung anzeigen *klick*)’ style=’blue’ collapse_link=’true’]
1.) $f'(x)$ und $f^{\prime\prime}(x)$ bilden
$f(x)=3x^2+6$
$f'(x)=6x$
$f^{\prime\prime}(x)=6$
2.) notwendige Bedingung $f'(x)=0$
\begin{align*}6x&=0&&\color{red}|\color{red}:\color{red}6\\
x&=0
\end{align*}
3.) hinreichende Bedingung $f^{\prime\prime}(x) \neq 0$
\begin{align*}
&&f^{\prime\prime}(x)&=6\\
&&f^{\prime\prime}(0)&=6&& \color{red}>\color{red}0\color{red}\rightarrow \color{red}T\color{red}P
\end{align*}
4.) y-Koordinate berechnen
$f(0)=3\cdot0^2+6=6\rightarrow TP(0/6)$
[/spoiler]
[spoiler title=’ 2. Berechne die Extrema von $f(x)=x^3+9x^2+1$ (Lösung anzeigen *klick*)’ style=’blue’ collapse_link=’true’]
1.) $f'(x)$ und $f^{\prime\prime}(x)$ bilden
$f(x)=x^3+9x^2+1$
$f'(x)=3x^2+18x$
$f^{\prime\prime}(x)=6x+18$
2.) notwendige Bedingung $f'(x)=0$
\begin{align*}3x^2+18x&=0&&&& \color{red}|\color{red}(\color{red})\\
x\cdot(3x+18)&=0&&&& \color{red}|\color{red}S\color{red}v\color{red}N\color{red}P\end{align*}
\begin{align*}&x=0&3x+18&=0&&\color{red}|\color{red}-\color{red}1\color{red}8\\
&&3x&=-18&&\color{red}|\color{red}:\color{red}3\\&&x&=-6
\end{align*}
3.) hinreichende Bedingung $f^{\prime\prime}(x) \neq 0$
\begin{align*}
f^{\prime\prime}(x)&=6x+18\\
f^{\prime\prime}(0)&=6\cdot0+18=18&&\color{red}>\color{red}0\color{red}\rightarrow \color{red}T\color{red}P\\
f^{\prime\prime}(-6)&=6\cdot(-6)+18=-18&&\color{red}<\color{red}0 \color{red}\rightarrow \color{red}H\color{red}P
\end{align*}
4.) y-Koordinate berechnen
$f(0)=0^3+9\cdot0^2+1=1 \hspace{1cm}\rightarrow TP(0/1)\\$
$f(-6)=(-6)^3+9\cdot(-6)^2+1=109\hspace{1cm}\rightarrow HP(-6/109)$
[/spoiler]
Zusammenfassung:
Extrema = Hoch-/Tiefpunkte
Entscheidungsregel:[one_third] Hochpunkt $\rightarrow$ [/one_third][two_third_last]$f'(x)=0$ und $f^{\prime\prime}(x)<0$[/two_third_last][one_third]Tiefpunkt $\rightarrow$[/one_third][two_third_last]$f'(x)=0$ und $f^{\prime\prime}(x)>0$[/two_third_last]
