Die drei binomischen Formeln Die erste binomische Formel Die zweite binomische Formel Die dritte binomische Formel
(1.) Die drei binomischen Formeln
Die erste binomische Formel:
$$(a+b)^2=a^2+2 \cdot a \cdot b + b^2 \text{ oder }$$
$$((1.)+(2.))^2=(1.)^2+2 \cdot (1.) \cdot (2.) + (2.)^2$$
Die zweite binomische Formel:
$$(a-b)^2=a^2-2 \cdot a \cdot b + b^2 \text{ oder }$$
$$((1.)-(2.))^2=(1.)^2-2 \cdot (1.) \cdot (2.) + (2.)^2$$
Die dritte binomische Formel:
$$(a+b) \cdot (a-b) =a^2 – b^2 \text{ oder }$$
$$((1.)+(2.)) \cdot ((1.)-(2.))=(1.)^2-(2.)^2$$
(2.) Die erste binomische Formel
a) Die Formel: \((a+b)^2=a^2+2 \cdot a \cdot b + b^2\)
b) Rechnerische Herleitung:
\( \begin{array}[h]{rl}
(a+b)^2 & =(a+b) \cdot (a+b) \, \,\, \,\, \,\, \,\, \,\, \,\, \, \text{ |ausklammern des linken Faktors}\\
& =a \cdot a + a \cdot b + b \cdot a + b \cdot b \\
& =a^2 + 2 \cdot a\cdot b +b^2 \
\end{array}\)
“Jedes Teil des ersten Ausdrucks mit jedem Teil der zweiten Klammer multiplizieren!”
c) Graphische Herleitung:
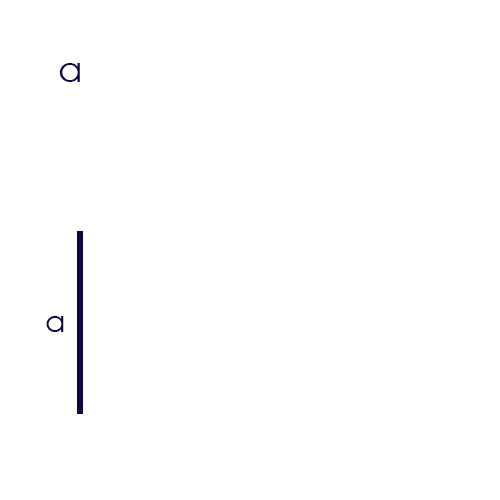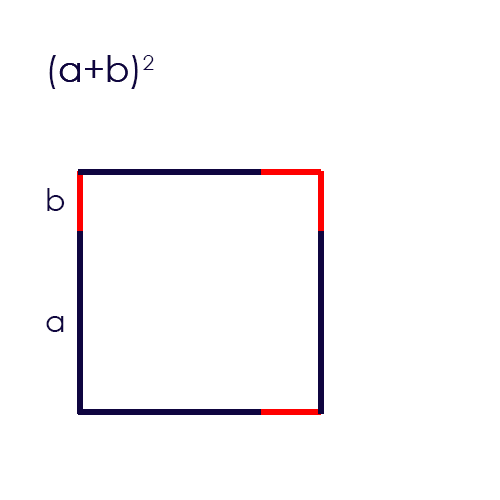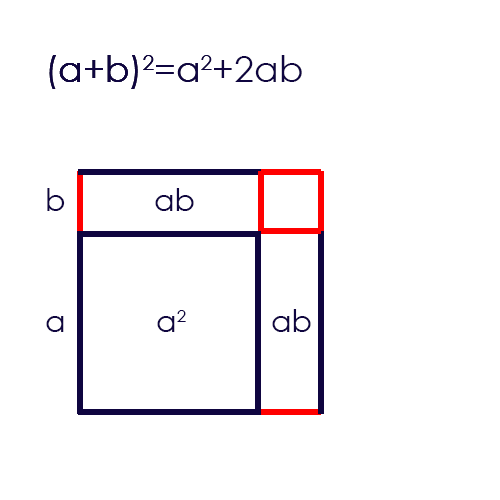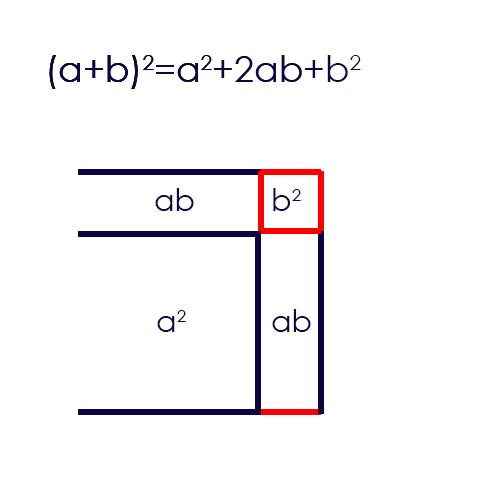
d) Beispiel Ausmultiplizieren:
\( \begin{array}[h]{rl}
(a+b)^2 & =a^2+2 \cdot a \cdot b +b^2 \\
(2x+5)^2 &=(2x)^2+ 2 \cdot 2x \cdot 5 + 5^2 \\
& =4x^2 + 2 \cdot 2 \cdot 5 \cdot x +25 \\
&=4x^2 + 20x +25
\end{array}\)
Natürlich kannst du mit einiger Übung die mittleren Rechenschritte weglassen und direkt von der Klammer zum endgültigen, vereinfachten Term gelangen!
e) Beispiel Faktorisieren:
\( \begin{array}[h]{rl}
a^2+2 \cdot a \cdot b +b^2 &=(a+b)^2 \\
9x^2+12xy+4y^2 &=(3x)^2+ 2 \cdot 3x \cdot 2y + (2y)^2 \\
& =(3x+2y)^2
\end{array}\)
Auch beim Faktorisieren kannst du direkt den vereinfachten Term hinschreiben!
Tipp: \( 9x^2+12xy+4y^2 \)
1. Wurzel aus \( 9x^2= \sqrt{9 \cdot x^2}=\sqrt{9} \cdot \sqrt{x^2}=3 \cdot x =3x\)
2. Wurzel aus \(4y^2=\sqrt{4 \cdot y^2}=\sqrt{4}\cdot \sqrt{y^2}=2y \)
3. Probe für den mittleren Teil: \( 2 \cdot 3x \cdot 2y=12xy\)
4. Anwenden
$$9x^2+12xy+4y^2=(3x+2y)^2$$
(3.) Die zweite binomische Formel
a) Die Formel: \((a-b)^2=a^2-2 \cdot a \cdot b + b^2\)
b) Rechnerische Herleitung:
\( \begin{array}[h]{rl}
(a-b)^2 & =(a-b) \cdot (a-b) \, \,\, \,\, \,\, \,\, \,\, \,\, \, \text{ |ausklammern des linken Faktors}\\
& =a \cdot a – a \cdot b – b \cdot a + b \cdot b \\
& =a^2 – 2 \cdot a\cdot b +b^2 \
\end{array}\)
“Jedes Teil des ersten Ausdrucks mit jedem Teil der zweiten Klammer multiplizieren!”
c) Graphische Herleitung:
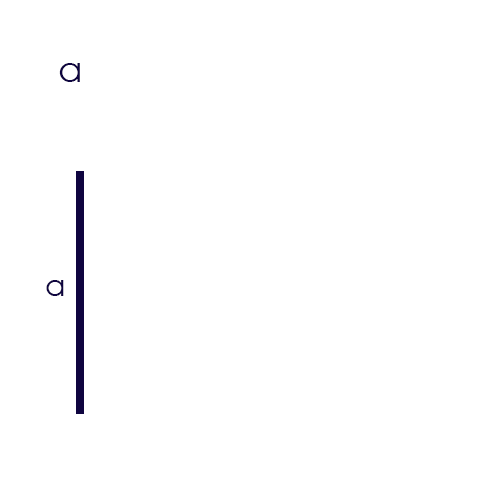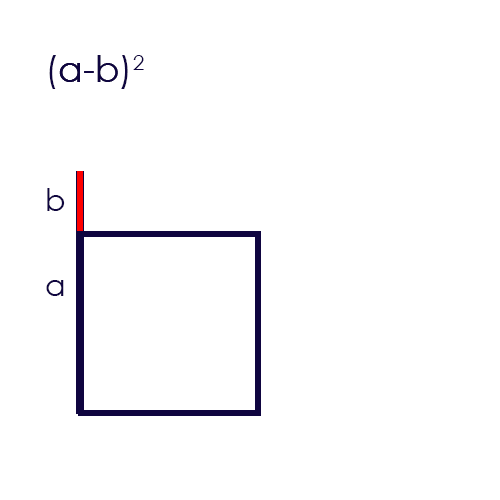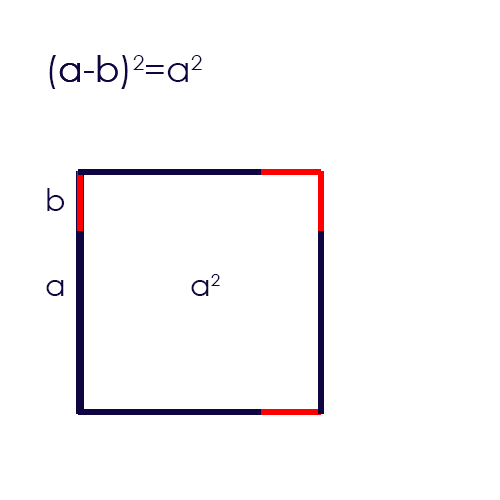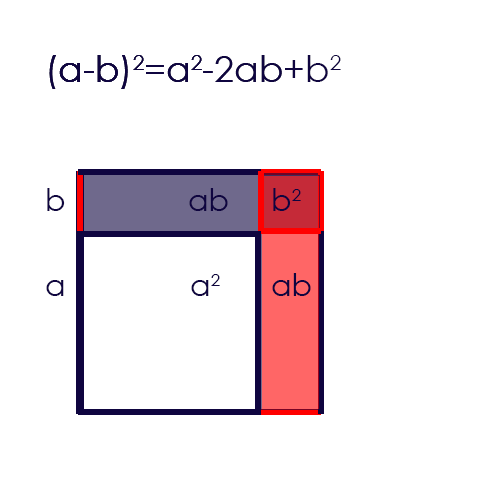
d) Beispiel Ausmultiplizieren:
\( \begin{array}[h]{rl}
(a – b)^2 & =a^2 – 2 \cdot a \cdot b + b^2 \\
(4x – 2y)^2 &=(4x)^2 – 2 \cdot 4x \cdot 2y + (2y)^2 \\
& =16x^2 – 2 \cdot 4 \cdot2 \cdot x \cdot y + 4y^2 \\
&=16x^2 – 16xy + 4y^2
\end{array}\)
Auch hier kannst du natürlich mit einiger Übung die mittleren Rechenschritte weglassen und direkt von der Klammer zum endgültigen, vereinfachten Term gelangen!
e) Beispiel Faktorisieren:
\( \begin{array}[h]{rl}
a^2 – 2 \cdot a \cdot b + b^2 & = (a – b)^2 \\
4x^2 – 20xy + 25y^2 &= (2x)^2 + 2 \cdot 2x \cdot 5y + (5y)^2 \\
& =(2x+5y)^2
\end{array}\)
Auch beim Faktorisieren kannst du direkt den vereinfachten Term hinschreiben!
Tipp: \( 4x^2 – 20xy + 25y^2 \)
1. Wurzel aus \( 4x^2= \sqrt{4 \cdot x^2}=\sqrt{4} \cdot \sqrt{x^2}=2 \cdot x =2x\)
2. Wurzel aus \(25y^2=\sqrt{25 \cdot y^2}=\sqrt{25}\cdot \sqrt{y^2}=5y \)
3. Probe für den mittleren Teil: \( 2 \cdot 2x \cdot 5y=20xy\)
4. Anwenden
$$4x^2 – 20xy + 25y^2=(2x – 5y)^2$$
(4.) Die dritte binomische Formel
a) Die Formel: \((a+b) – (a – b)=a^2 – b^2\)
b) Rechnerische Herleitung:
\( \begin{array}[h]{rl}
(a+b)\cdot (a-b) &=a \cdot a – a \cdot b + b \cdot a – b \cdot b \, \,\, \,\, \,\, \,\, \,\, \,\, \, \text{ |ausklammern des linken Faktors}\\
& =a^2 – b^2 \
\end{array}\)
“Jedes Teil des ersten Ausdrucks mit jedem Teil der zweiten Klammer multiplizieren!”
c) Graphische Herleitung:
d) Beispiel Ausmultiplizieren:
\( \begin{array}[h]{rl}
(a+b)(a – b) & =a^2-b^2 \\
(2y+4b)(2y – 4b) &=(2y)^2 – (4b)^2 \\
& =2y \cdot 2y – 4b \cdot 4b \\
&=2 \cdot 2 \cdot y \cdot y – 4 \cdot 4 \cdot b \cdot b\\
&=4y^2 – 16b^2
\end{array}\)
e) Beispiel Faktorisieren:
\( \begin{array}[h]{rl}
a^2 – b^2 &=(a+b)(a-b) \\
9x^2-100y^2 &=(3x+10y)(3x-10y)
\end{array}\)
Tipp: \( 9x^2-100y^2 \)
1. Wurzel aus \( 9x^2= \sqrt{9 \cdot x^2}=\sqrt{9} \cdot \sqrt{x^2}=3 \cdot x =3x\)
2. Wurzel aus \(100y^2=\sqrt{100 \cdot y^2}=\sqrt{100}\cdot \sqrt{y^2}=10 \cdot y=10y \)
3. Anwenden
$$9x^2-100y^2=(3x+10y)(3x-10y)$$
