(1.) Was ist ein Baumdiagramm
(2.) Ziehen mit Zurücklegen
(3.) Ziehen ohne Zurücklegen
(4.) Pfad- und Summenregel
(1.) Was ist ein Baumdiagramm
Das Baumdiagramm ist eine übersichtliche Darstellungsmöglichkeit von mehrstufigen Zufallsexperimenten. Es gibt nicht nur die verschiedenen Wahrscheinlichkeiten, sondern auch die möglichen Ausgänge eines solchen Experimentes an.
Grundsätzlich unterscheidet man hier zwischen Baumdiagrammen, die ein Zufallsexperiment für “Ziehen mit Zurücklegen” und “Ziehen ohne Zurücklegen” darstellen.
(2.) Ziehen mit Zurücklegen
Bei einem Baumdiagramm, welches ein solches Zufallsexperiment repräsentiert, eignet sich das Ziehen von Kugel aus einer Urne, besonders gut! Hierbei wird die erste gezogene Kugel wieder zurückgelegt, sodass bei jeder Stufe die Ausgangssituation wieder hergestellt wird.
Beispiel: In einer Urne sind 3 schwarze und 2 rote Kugeln. Es wird zweimal “mit Zurücklegen” gezogen. Die Wahrscheinlichkeiten sind:
\(P(“schwarze \, Kugel”)= \frac{3}{5}\), da 3 von 5 Kugeln schwarz sind und
\(P(“rote \, Kugel”)= \frac{2}{5}\), da 2 von 5 Kugeln schwarz sind.
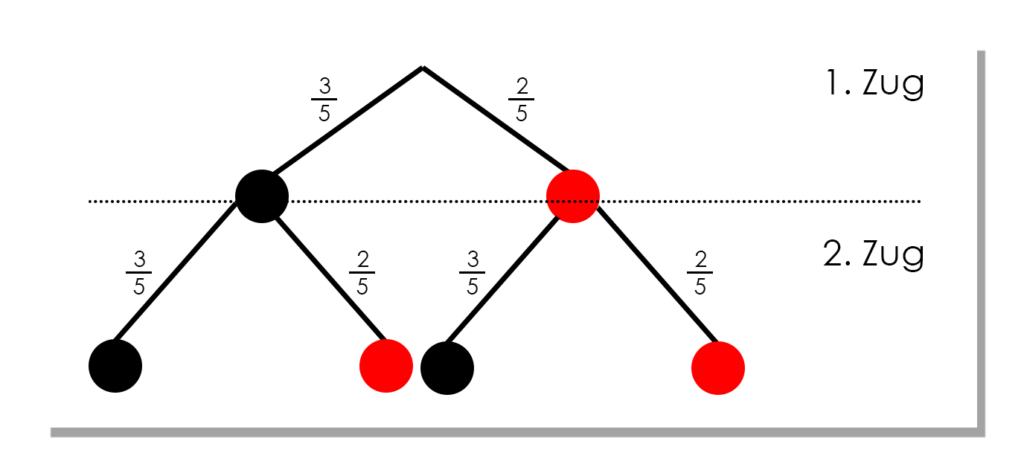
Berechnung der Endwahrscheinlichkeiten mithilfe der Pfadregel:
\(P(“Im \, ersten \, und \,im \, zweiten\, Zug \, eine \, schwarze \, Kugel”)=\frac{3}{5} \cdot \frac{3}{5}=\frac{9}{25}\)
\(P(“Im \, ersten\, Zug \,schwarz \, und \,im \, zweiten\, Zug \, eine \,rote \, Kugel”)=\frac{3}{5} \cdot \frac{2}{5}=\frac{6}{25}\)
\(P(“Im \, ersten\, Zug \, rot \, und \,im \, zweiten\, Zug \, eine \, schwarze \, Kugel”)=\frac{2}{5} \cdot \frac{3}{5}=\frac{6}{25}\)
\(P(“Im \, ersten \, und \,im \, zweiten\, Zug \, eine \, rote \, Kugel”)=\frac{2}{5} \cdot \frac{2}{5}=\frac{4}{25}\)

Tipp: Du kannst deine Endwahrscheinlichkeiten kontrollieren, in dem du sie addierst. Sie müssen zusammen 1 ergeben!
\(\frac{9}{25}+\frac{6}{25}+\frac{6}{25}+\frac{4}{25}=\frac{25}{25}=1\)
(3.) Ziehen ohne Zurücklegen
Bei einem Baumdiagramm, welches ein solches Zufallsexperiment darstellt, wird im Gegensatz zu “Ziehen mit Zurücklegen” die erste gezogene Kugel nicht wieder in die Urne zurückgelegt, sodass sich die Wahrscheinlichkeiten ab der 2. Stufe von der Ausgangssituation unterscheiden. Die Gesamtzahl ändert sich!
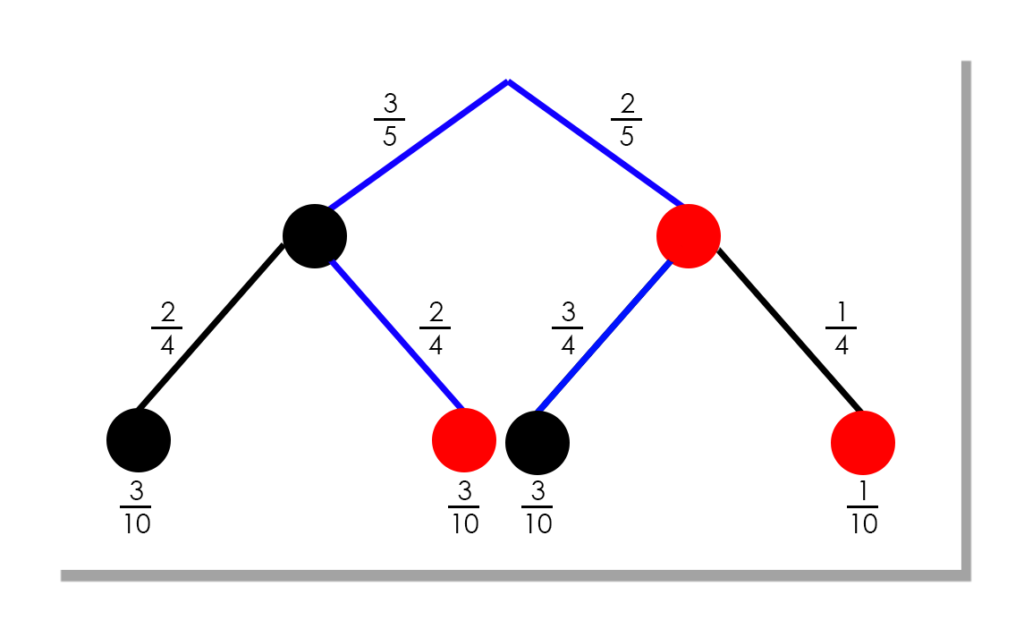
Beispiel: In einer Urne sind 3 schwarze und 2 rote Kugeln. Es wird zweimal “ohne Zurücklegen” gezogen:

Berechnung der Endwahrscheinlichkeiten mithilfe der Pfadregel:
\(P(“Im \, ersten \, und \,im \, zweiten\, Zug \, eine \, schwarze \, Kugel”)=\frac{3}{5} \cdot \frac{2}{4}=\frac{6}{20}=\frac{3}{10}\)
\(P(“Im \, ersten\, Zug \,schwarz \, und \,im \, zweiten\, Zug \, eine \,rote \, Kugel”)=\frac{3}{5} \cdot \frac{2}{4}=\frac{6}{20}=\frac{3}{10}\)
\(P(“Im \, ersten\, Zug \, rot \, und \,im \, zweiten\, Zug \, eine \, schwarze \, Kugel”)=\frac{2}{5} \cdot \frac{3}{4}=\frac{6}{20}=\frac{3}{10}\)
\(P(“Im \, ersten \, und \,im \, zweiten\, Zug \, eine \, rote \, Kugel”)=\frac{2}{5} \cdot \frac{1}{4}=\frac{2}{20}=\frac{1}{10}\)

Auch hier gilt: Die Endwahrscheinlichkeiten müssen zusammen 1 ergeben:
\(\frac{3}{10}+\frac{3}{10}+\frac{3}{10}+\frac{1}{10}=\frac{10}{10}=1\)
(4.) Pfad- und Summenregel
- Pfadregel:
Entlang eines Pfades (Astes) wird multipliziert. Das Ergebnis gibt die Wahrscheinlichkeit für einen bestimmten Versuchsausgang an. - Summenregel:
Wenn die Wahrscheinlichkeit eines Ereignisses (Versuchsausgang) gesucht wird, das mehrere Pfade beinhaltet, werden die jeweiligen Endwahrscheinlichkeiten addiert.
Beispiel: \(P(“eine\, schwarze \, Kugel”)\)
\(P(“eine\, schwarze \, Kugel”)=\frac{3}{10}+\frac{3}{10}=\frac{6}{10}=\frac{3}{5}\)

