In diesem Artikel erkläre ich dir was die Wahrscheinlichkeitsverteilung ist, wie man sie erstellt und natürlich auch wofür sie dient. Die Wahrscheinlichkeitsverteilung wird oft auch einfach nur Verteilung genannt. Hierzu werde ich sie zunächst mathematisch definieren und sie anschließend an einem einfachen Beispiel erklären. Als letztes gibt es noch hilfreiche Tipps zur Erstellung!
Was du vorher wissen solltest:

 Aufgabentext: Stell dir bitte diese Hündin namens Ria vor. Ria bekommt drei Welpen. Die Wahrscheinlichkeit für die Geburt eines Rüden beträgt 40%. Die Zufallsgröße X beschriebt die Anzahl an männlichen Nachkommen, die diese Hündin bekommt.
Aufgabenstellung: Stelle für diesen Sachverhalt eine Wahrscheinlichkeitsverteilung auf!
Lösung: Die Wahrscheinlichkeitsverteilung lässt sich immer besonders gut als eine Tabelle darstellen, die in der ersten Zeile die möglichen Ausprägungen der Zufallsgröße X hat und in der zweiten Zeile die zugehörigen Wahrscheinlichkeiten.
Aus der Aufgabenstellung entnehmen wir was die Zufallsgröße X ist. In diesem Fall die Anzahl an männlichen Nachkommen. Hier müssen wir uns nun überlegen wieviele Rüden diese Hündin bekommen kann, wenn sie denn 3 Junge bekommt. Sie kann doch keinen Rüden bekommen, also Null (und diese Null wird häufig vergessen!), einen, zwei oder drei Rüden. Genau mit diesen Zahlen beschriften wir die obere Zeile der Tabelle!
Aufgabentext: Stell dir bitte diese Hündin namens Ria vor. Ria bekommt drei Welpen. Die Wahrscheinlichkeit für die Geburt eines Rüden beträgt 40%. Die Zufallsgröße X beschriebt die Anzahl an männlichen Nachkommen, die diese Hündin bekommt.
Aufgabenstellung: Stelle für diesen Sachverhalt eine Wahrscheinlichkeitsverteilung auf!
Lösung: Die Wahrscheinlichkeitsverteilung lässt sich immer besonders gut als eine Tabelle darstellen, die in der ersten Zeile die möglichen Ausprägungen der Zufallsgröße X hat und in der zweiten Zeile die zugehörigen Wahrscheinlichkeiten.
Aus der Aufgabenstellung entnehmen wir was die Zufallsgröße X ist. In diesem Fall die Anzahl an männlichen Nachkommen. Hier müssen wir uns nun überlegen wieviele Rüden diese Hündin bekommen kann, wenn sie denn 3 Junge bekommt. Sie kann doch keinen Rüden bekommen, also Null (und diese Null wird häufig vergessen!), einen, zwei oder drei Rüden. Genau mit diesen Zahlen beschriften wir die obere Zeile der Tabelle!
 Nun suchen wir die zugehörigen Wahrscheinlichkeiten!
Als erstes beginnen wir mit der Wahrscheinlichkeit für 0 Rüden!
Nun suchen wir die zugehörigen Wahrscheinlichkeiten!
Als erstes beginnen wir mit der Wahrscheinlichkeit für 0 Rüden!
 Da wir nun die Wahrscheinlichkeit für 0 Rüden suchen, also für drei Weibchen, betrachten wir den äußeren Ast.
Da wir nun die Wahrscheinlichkeit für 0 Rüden suchen, also für drei Weibchen, betrachten wir den äußeren Ast.
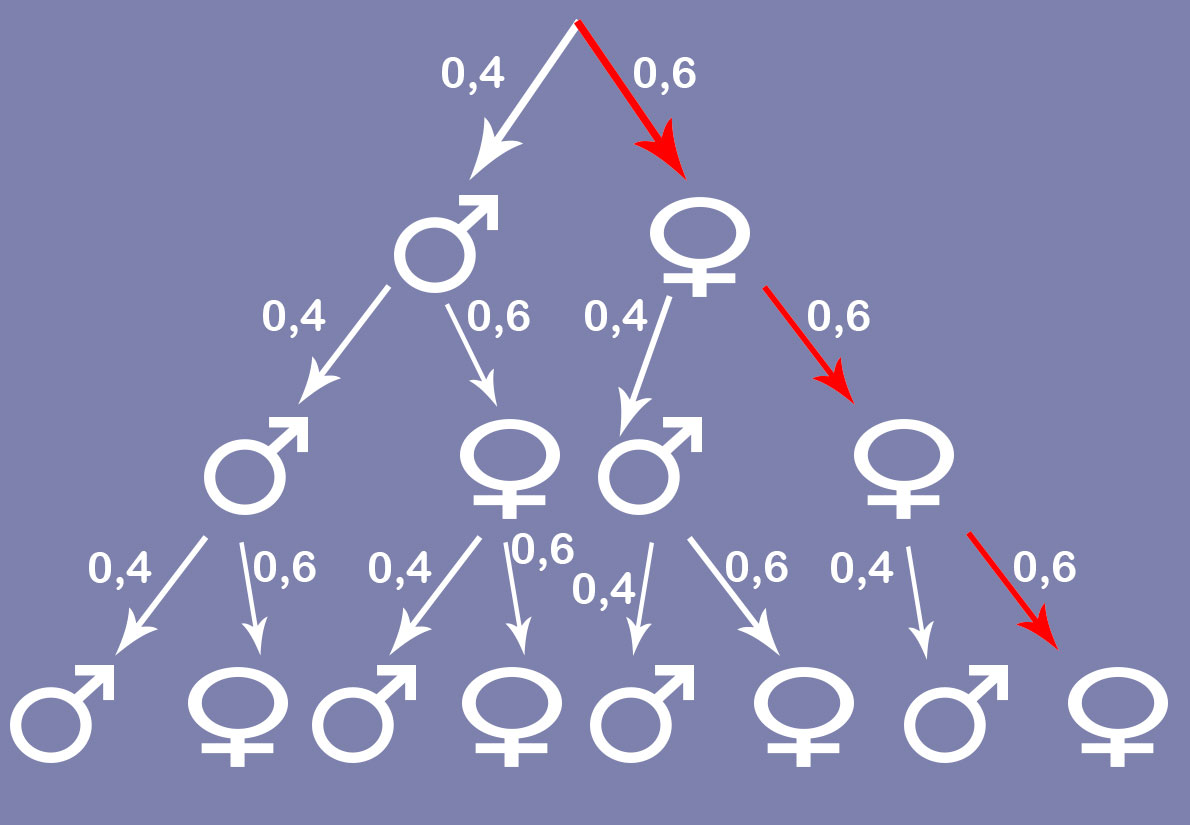 Wir rechnen also:
Wir rechnen also:
 Genauso gehen wir jetzt bei der Suche nach der Wahrscheinlichkeit für einen, zwei und drei Rüden vor.
Ich mache es dir noch einmal für einen Rüden vor!
Genauso gehen wir jetzt bei der Suche nach der Wahrscheinlichkeit für einen, zwei und drei Rüden vor.
Ich mache es dir noch einmal für einen Rüden vor!
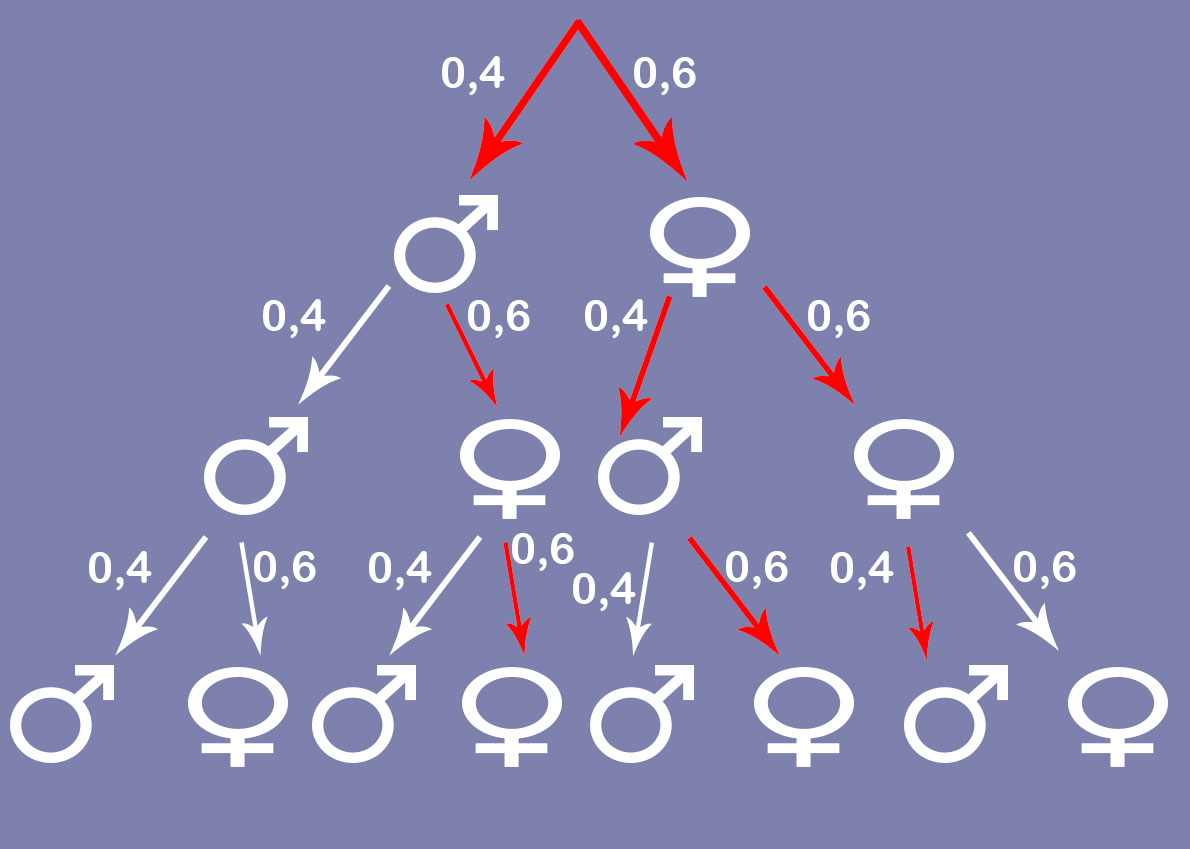 Wie du siehst, suchen wir nun die Wahrscheinlichkeit von diesen drei Ästen!
P(m,w,w) + P(w,m,w) + P(w,w,m)
= 3 • 0,4 • 0,6 • 0,6 = 0,432
Jeder einzelne Ast hat die Wahrscheinlichkeit 0,4 • 0,6 • 0,6, also konnte ich diese Wahrscheinlichkeit mit 3 multiplizieren (in der Multiplikation gilt das Kommutativgesetz!).
Auch diese Zahl wird in die Tabelle eingetragen. Da es dir Wahrscheinlichkeit von einem Rüden war, trage ich die 0,432 direkt unter die 1 ein:
Wie du siehst, suchen wir nun die Wahrscheinlichkeit von diesen drei Ästen!
P(m,w,w) + P(w,m,w) + P(w,w,m)
= 3 • 0,4 • 0,6 • 0,6 = 0,432
Jeder einzelne Ast hat die Wahrscheinlichkeit 0,4 • 0,6 • 0,6, also konnte ich diese Wahrscheinlichkeit mit 3 multiplizieren (in der Multiplikation gilt das Kommutativgesetz!).
Auch diese Zahl wird in die Tabelle eingetragen. Da es dir Wahrscheinlichkeit von einem Rüden war, trage ich die 0,432 direkt unter die 1 ein:
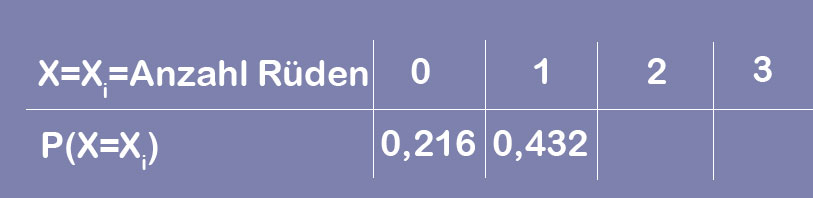 Die vollständig ausgefüllte Tabelle sieht dann so aus:
Die vollständig ausgefüllte Tabelle sieht dann so aus:
 Hier siehst du nochmal alle Rechnungen auf einen Blick:
Hier siehst du nochmal alle Rechnungen auf einen Blick:
 Diese ausgefüllte Tabelle nennt man Wahrscheinlichkeitsverteilung!
Diese ausgefüllte Tabelle nennt man Wahrscheinlichkeitsverteilung!
Mathematische Definition einer Wahrscheinlichkeitsverteilung:

Erklärung der Wahrscheinlichkeitsverteilung an einem Beispiel:
 Aufgabentext: Stell dir bitte diese Hündin namens Ria vor. Ria bekommt drei Welpen. Die Wahrscheinlichkeit für die Geburt eines Rüden beträgt 40%. Die Zufallsgröße X beschriebt die Anzahl an männlichen Nachkommen, die diese Hündin bekommt.
Aufgabenstellung: Stelle für diesen Sachverhalt eine Wahrscheinlichkeitsverteilung auf!
Lösung: Die Wahrscheinlichkeitsverteilung lässt sich immer besonders gut als eine Tabelle darstellen, die in der ersten Zeile die möglichen Ausprägungen der Zufallsgröße X hat und in der zweiten Zeile die zugehörigen Wahrscheinlichkeiten.
Aus der Aufgabenstellung entnehmen wir was die Zufallsgröße X ist. In diesem Fall die Anzahl an männlichen Nachkommen. Hier müssen wir uns nun überlegen wieviele Rüden diese Hündin bekommen kann, wenn sie denn 3 Junge bekommt. Sie kann doch keinen Rüden bekommen, also Null (und diese Null wird häufig vergessen!), einen, zwei oder drei Rüden. Genau mit diesen Zahlen beschriften wir die obere Zeile der Tabelle!
Aufgabentext: Stell dir bitte diese Hündin namens Ria vor. Ria bekommt drei Welpen. Die Wahrscheinlichkeit für die Geburt eines Rüden beträgt 40%. Die Zufallsgröße X beschriebt die Anzahl an männlichen Nachkommen, die diese Hündin bekommt.
Aufgabenstellung: Stelle für diesen Sachverhalt eine Wahrscheinlichkeitsverteilung auf!
Lösung: Die Wahrscheinlichkeitsverteilung lässt sich immer besonders gut als eine Tabelle darstellen, die in der ersten Zeile die möglichen Ausprägungen der Zufallsgröße X hat und in der zweiten Zeile die zugehörigen Wahrscheinlichkeiten.
Aus der Aufgabenstellung entnehmen wir was die Zufallsgröße X ist. In diesem Fall die Anzahl an männlichen Nachkommen. Hier müssen wir uns nun überlegen wieviele Rüden diese Hündin bekommen kann, wenn sie denn 3 Junge bekommt. Sie kann doch keinen Rüden bekommen, also Null (und diese Null wird häufig vergessen!), einen, zwei oder drei Rüden. Genau mit diesen Zahlen beschriften wir die obere Zeile der Tabelle!
 Nun suchen wir die zugehörigen Wahrscheinlichkeiten!
Als erstes beginnen wir mit der Wahrscheinlichkeit für 0 Rüden!
Nun suchen wir die zugehörigen Wahrscheinlichkeiten!
Als erstes beginnen wir mit der Wahrscheinlichkeit für 0 Rüden!
P(X=0):
Als kleine Hilfe können wir ein Baumdiagramm zeichnen. Da wir nun die Wahrscheinlichkeit für 0 Rüden suchen, also für drei Weibchen, betrachten wir den äußeren Ast.
Da wir nun die Wahrscheinlichkeit für 0 Rüden suchen, also für drei Weibchen, betrachten wir den äußeren Ast.
 Wir rechnen also:
Wir rechnen also:
P(w,w,w) = 0,6 • 0,6 • 0,6 = 0,63 = 0,216
Diese Wahrscheinlichkeit tragen wir in die Tabelle unter die Null ein, da sie die Wahrscheinlichkeit für Null Rüden ist. Genauso gehen wir jetzt bei der Suche nach der Wahrscheinlichkeit für einen, zwei und drei Rüden vor.
Ich mache es dir noch einmal für einen Rüden vor!
Genauso gehen wir jetzt bei der Suche nach der Wahrscheinlichkeit für einen, zwei und drei Rüden vor.
Ich mache es dir noch einmal für einen Rüden vor!
P(X=1):
Wir suchen zunächst am Baumdiagramm die passenden Äste: Wie du siehst, suchen wir nun die Wahrscheinlichkeit von diesen drei Ästen!
P(m,w,w) + P(w,m,w) + P(w,w,m)
= 3 • 0,4 • 0,6 • 0,6 = 0,432
Jeder einzelne Ast hat die Wahrscheinlichkeit 0,4 • 0,6 • 0,6, also konnte ich diese Wahrscheinlichkeit mit 3 multiplizieren (in der Multiplikation gilt das Kommutativgesetz!).
Auch diese Zahl wird in die Tabelle eingetragen. Da es dir Wahrscheinlichkeit von einem Rüden war, trage ich die 0,432 direkt unter die 1 ein:
Wie du siehst, suchen wir nun die Wahrscheinlichkeit von diesen drei Ästen!
P(m,w,w) + P(w,m,w) + P(w,w,m)
= 3 • 0,4 • 0,6 • 0,6 = 0,432
Jeder einzelne Ast hat die Wahrscheinlichkeit 0,4 • 0,6 • 0,6, also konnte ich diese Wahrscheinlichkeit mit 3 multiplizieren (in der Multiplikation gilt das Kommutativgesetz!).
Auch diese Zahl wird in die Tabelle eingetragen. Da es dir Wahrscheinlichkeit von einem Rüden war, trage ich die 0,432 direkt unter die 1 ein:
 Die vollständig ausgefüllte Tabelle sieht dann so aus:
Die vollständig ausgefüllte Tabelle sieht dann so aus:
 Hier siehst du nochmal alle Rechnungen auf einen Blick:
Hier siehst du nochmal alle Rechnungen auf einen Blick:
 Diese ausgefüllte Tabelle nennt man Wahrscheinlichkeitsverteilung!
Diese ausgefüllte Tabelle nennt man Wahrscheinlichkeitsverteilung!
Hilfreiche Tipps zur Erstellung einer Wahrscheinlichkeitsverteilung:
1. Du musst nicht unbedingt ein Baumdiagramm erstellen. Wenn du es kannst, dann reicht es wenn du die Kombinationsmöglichkeiten aufschreibt und davon dann die Wahrscheinlichkeiten bestimmst, diese addierst und dann in die Tabelle einträgst. (So wie ich es auf dem Bild hier drüber gemacht habe) 2. Du kannst deine Wahrscheinlichkeiten überprüfen, denn addiert müssen sie 1 ergeben. Hier also:0,216 + 0,432 + 0,288 + 0,064 = 1
3. Genau genommen reicht es, wenn du alle Wahrscheinlichkeiten bis auf eine bestimmst, denn diese anderen kannst du von der 1 abziehen und erhältst die letzte Wahrscheinlichkeit! 4. Die äußeren Wahrscheinlichkeiten sind immer leichter zu bestimmen, da sie häufig nur mit Hilfe eines Astes eines Baumdiagramms berechnet werden. Wenn du also den dritten Tipp berücksichtigst, dann würde ich ein Feld in der Mitte frei lassen und seine Wahrscheinlichkeit mit Hilfe des Tricks bestimmen!Video auf Youtube anschauen: >>>Hier klicken<<<
Machst du nächstes Jahr dein Abitur und suchst nach einer Unterstützung?
Dann schau dir unsere Abikurse an!




